Summary
We implemented two abortable locks, MCS time published lock and CLH try lock. We compared it with test and set lock and CLH queue lock. All lock implementations were run on the GHC machine and then had metrics collected for analysis.
Background
In 15418/618 we studied two types of locks. The first type belongs to test and set and its variants which are very simple to implement but they do not scale well due to the increase in interconnect traffic they generate and their unfairness towards the lock requestors. The second type belongs to array locks and its variants. These locks are good with fairness and reduce unnecessary interconnect traffic but they have a strict FIFO ordering for granting the locks which makes it perform worse in the event of preemption (especially when number of threads is more than number of cores in the machine).
We implemented and analyzed the third variant of locks called the abortable locks. The abortable locks which are built from the basic queue based locks don't impose the strict FIFO ordering like the queue based locks which helps it to handle preemption and also helps it to scale well due to better fairness compared to the tas locks and its variants. Other than this, these locks can also be used in applications like real-time systems where there is a strict deadline/timing requirements in place and the thread can't simply spin and wait to acquire the lock for unbounded time.
We performed the analysis on a GHC machine which compares the abortable locks with the other two types of locks and explains the advantages and disadvantages. We used GHC as we are familiar with this system.
The locks that we implemented, tested were test-and-set, mcs, mcs - time published (mcs-tp), clh, clh-try, test-and-set backoff, test-and-test-and-set, test-and-test-and-set backoff, array and ticket locks. But we have used only test-and-set, mcs - time published (mcs-tp), clh, clh-try for our analysis.
The locks which we used for our analysis are given below:
Locks
TAS
This is the simple Test and set lock which was taught in class. We implemented this in assembly using the lock bts instruction. We considered using this lock in our analysis as this lock doesn’t scale well and has a lot of unfairness inbuilt to it.
The MCS-TP is a queue-based lock which is built using the basic MCS queue lock but with more features to it. As we saw in the previous section, the clh-try lock can help in the phase of preemption by timing out and performing an alternate execution path or simply checking for lock holder’s preemption (performing a yield if needed) and later retrying and rejoining the queue.
Even though it does all these, there can be two cases which can be a challenge to the clh-try lock. What if there is no alternate execution path and the critical section has to be executed? Most probably this is the case in general purpose codes. What if not the lock holder but the other nodes (especially the one next in line to acquire the lock) waiting for the lock gets preempted?
The MCP-TP handles these cases by a feature called “time publishing” alongwith the timeout and lock holder preemption techniques similar to the clh-try lock.
Time publishing is the method by which a waiting node keeps writing the current wall-clock time to a global variable frequently. As a result of this the lock holder (when trying to do a release) can identify whether a waiting queue node is preempted by checking if the last timestamp published by the node is stale (not recent enough).
As shown in the state transition diagram above the MCS-TP lock inherits the original waiting and available states from the MCS queue lock. Along with it we have two more states called “left” (we call this timed_out in our code) and “removed”. The available state means the node has acquired the lock. The waiting state means the node is waiting for the lock to be available (until the lock holder passes it). The left (timed_out) state means the node has waited more than its PATIENCE and timed out. Unlike the clh-try lock, the timed out node doesn’t remove itself from the queue and can rejoin the queue later if the lock holder hasn’t removed it by then.
The removed state is given to a queue node by the lock holder while it attempts to release the lock. This happens in two scenarios as shown in the diagram above. The lock holder can remove the queue node if it observes that the node has a stale published timestamp or if the node has already timed out (and not yet rejoined the queue).
Apart from this the MCS-TP implementation has a parameter called MAX_NODES_TO_SCAN. This parameter specifies the upper bound for the number of steps involved in the lock release. For example if this parameter is 4, then the lock holder can scan upto 4 queue nodes before releasing the lock. It is possible for the lock holder to release the lock before 4 nodes, but after scanning 4 nodes the lock holder is forced to release the lock (regardless of the queue node’s state) in order to maintain the bound and forward progress of the program. This parameter can be tuned by the user in our implementation.

The CLH is a queue-based lock which provides fairness to the lock requestors and is similar to the MCS queue lock which was taught in the class. One main difference is that this lock has a previous pointer in the queue node’s structure and spins on the previous queue node’s state variable. It waits for the previous queue node to update its state variable on release (whereas in the MCS the lock holder updates the next queue node's state variable for release).
The disadvantage of this lock is that when the number of threads are more than the number of cores in the target machine, this lock doesn't perform well. This is because there is a possibility that threads waiting in the queue can get preempted and the lock holder may handover the lock to an inactive thread which makes all the threads waiting behind this lock to simply spin without the possibility of acquiring the lock (until the preempted thread becomes active again).
CLH-Try
Figure and caption courtesy of Michael L. Scott and William N. Scherer III from "Scalable Queue-Based Spin Locks with Timeout"
"Figure 6: The two principal cases in the CLH-try lock. In the figure at left process B can leave the middle of the queue as soon as it receives confirmation from its successor, C, that no pointer to its queue node remains. In the figure at right, B can leave the end of the queue once it has updated the tail pointer, Q, using compare and swap. The transitions from waiting to leaving and from waiting to available (not shown) must also be made with compare and swap, to avoid overwriting a transient flag."

The CLH-TRY is a variant of CLH lock. The special feature of this lock (compared to CLH) is that it is a timeout-based lock. So when a queue node keeps spinning in the queue for more than the timeout (user specified value) the queue node can leave from the queue.
To implement this feature, in addition to the two queue node states “waiting” and “available” from the CLH lock, we need three more states “leaving”, “transient” and “recycled” states.
As shown in the figure there are two possible cases when a node wants to leave the queue. The node can be in the middle of the queue or it can be in the end of the queue and both these cases are handled differently.
When in the middle of the queue the leaving node changes the left neighbour’s state to transient (using atomic compare exchange operation) and it marks its own node as leaving (using the atomic compare exchange operation). As soon as it changes its own state to leaving, the right neighbour which is spinning on this state observes that change and updates its prev pointer to the leaving node’s previous node. After doing this it changes the leaving node’s state from leaving to recycled to inform the leaving node that it is free to leave the queue. The leaving node then leaves the queue and updates the left neighbour’s state back to waiting just before it leaves. The right neighbour (of the node which left) spins on its new neighbour’s state. This process is explained in the figure shown above.
When the leaving node is at the end of the queue, the process is almost similar to the one explained above except for that the leaving node updates the lock tail pointer to point to its previous node (as there is no right neighbour in this case). The state transitions are also similar except for there is no need for a recycled state in this case (as there is no right neighbour in this case). This process is also explained in the figure shown above.
Apart from these changes there is an additional parameter called PATIENCE INTERVAL which is a user specified value. As discussed before, this simply tells the lock implementation how long a queue node can be spinning and waiting in the queue before timing out and leaving the queue.
What happens after timeout?
After a timeout happens, the thread can either execute an alternate execution path which does not depend on acquiring the lock or it can check whether the lock holder has been preempted and perform a yield. After performing one of these, the thread will retry for the lock and rejoin the queue. We tested both these possible implementations in our microbenchmarks.
How to check lock holder preemption?
Checking lock holder preemption was done using a special variable in the lock’s structure called “crit_sec_start_time”. This variable is reinitialized with wall_clock_time every time a thread acquires the lock. The queue nodes (who were waiting in the queue before) after being timed out check whether the current time is more than crit_sec_start_time + MAX_CS_TIME (maximum time to execute the critical section) + UPD_DELAY(average interconnect delay for one thread to observe another thread’s update). If this condition is satisfied then the thread(which has the timed out queue node) assumes that the lock holder is preempted and performs a yield in hopes of scheduling the lock holder back again.
Approach
We used C to code our locks because it allowed us to easily put in x86 assembly when needed using standard calling convention, and used GHC since we are familiar with this system.
Due to the nature of GHC, we know that the system has 8 cores, and so our tests exploit that through evaluating 4, 8, 16, and 32 threads. The 4 and 8 threads are cases where num_threads is less than or equal to num_cores whereas the 16 and 32 threads trigger lot of preemption as the num_threads is greater than num_cores.
We used the atomic_compare_exchange_weak() function (from the header file <stdatomic.h>) to perform the atomic compare and swap operations to implement the mcs, mcs-tp, clh and clh-try locks. We compiled the C codes with clang. As a side note, the lock implementations before the checkpoint (test and set, tas_with_backoff, test and test and set, tatas_with_backoff, ticket, array) were done in combination of assembly and C.
We also used the function sched_yield() from sched.h to perform the yield.
We used two different high resolution timers (with nanoseconds resolution) as our code depends on the correctness of timers. We called the timespec_get(&t0, TIME_UTC) to get the wall_clock_time and used it to time the system wide events like detecting lock holder preemption(in clh_try and mcs_tp) and time publishing (in mcs_tp). We also used the clock_gettime(CLOCK_THREAD_CPUTIMEID, &t0) to obtain the thread specific time which was used for determining whether a thread has timed out. We understood that wall_clock_time cannot be used for determining queue node’s timeout as we specifically need to determine how much time a thread spent waiting while it was active.
We used the perf tool to measure cache references of various lock implementations.
We used the pthread.h library to spawn the threads needed to test our locks.
We referred to the state transition diagrams, algorithm and pseudocode from the papers mentioned in the references.
Microbenchmarks
MB1
An empty critical section
MB2
A memory accessing critical section with an idle while-loop based non-critical section
MB3
A memory accessing critical section with NO non-critical section
MB4
Matrix multiplication with two small sized global arrays in the critical section
The parallelism is dependent on multiple pthreads running. Lock acquiring and releasing can become particularly expensive due to preemption due to more threads than the number of cores in the machine. There are also other factors that go into considering the time it takes for a lock to be acquired and released, such as critical section execution time, timeout, number of nodes to scan, and etc. These aforementioned parameters are particular to the lock implementations that we wrote.
What made our project difficult?
1.
The code needs to be race free. We had to consider what happens when some other thread changes our current thread’s state before we change our current thread’s state.
2.
We had to consider using volatile variables.
3.
Testing effects of preemption is hard as it changes every run because of the scheduler’s dynamic decisions. We had to do multiple runs to measure one value.
4.
Getting the timing right. Our lock implementations depend a lot on time, so using the right timers with high resolution was needed. Also we had to profile our critical section time for each microbenchmark as our code relies on those values.
5.
On top of all of these, we are reordering the linked list.
Results
The results that we collected were successful; to us this means that what we saw was to be expected (although there were some surprises!!). In addition to agreeing with our knowledge of these locks and how threading works, we confirmed the results of some of the tests with one of our references who did a similar series of tests.
We started by measuring each microbenchmarks runtime vs. threads. We also performed some additional tests. Some of the inferences that were made from observing the data are as follows.
Microbenchmark 1 (result shown above):
It consists of a while loop (spinning for 0.13s) critical section and while loop (spinning for 0.13s) non-critical section, together inside a bigger while loop to support retries and alternate execution path. This microbenchmark tries to test the timeout capability in clh-try and how it can be useful when we have an alternate execution path to execute in our code (https://github.com/apoltora/LocksProject/blob/af12bf815e287e2e2d75c8916bd74775ce9c0608/microbenchmarks/mb1/mb1_clh_try.c#L268).
Inference: We can see that clh_try (with patience equal to time of 3 critical sections) clearly wins compared to tas and clh, if there is an alternate execution path as the lock nodes which have been waiting for some time lose patience and start executing the non-critical section and make progress. They later retry an acquire after they finish executing the non-critical section. Whereas in tas and clh only the lock holders can make progress and the waiting nodes still wait for acquiring the lock in spite of there being an alternate execution path.
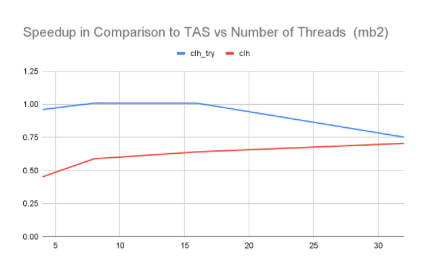
Microbenchmark 2 (result shown above):
10000000 array elements accessing critical section with while loop (spinning for some time) non-critical section, together inside a bigger while loop to support retries and alternate execution path.https://github.com/apoltora/LocksProject/blob/af12bf815e287e2e2d75c8916bd74775ce9c0608/microbenchmarks/mb2/mb2_clh_try.c#L278. This microbenchmark tries to test the timeout capability in clh-try and how it can be useful when we have an alternate execution path to execute in our code.
Inference: In the above graph also we can see that the clh_try (with patience equal to time of 3 critical sections) performs better than clh due to its timeout capability till 16 threads. At 32 threads there is a possibility the clh_try lock’s nodes couldn't leave the queue because the neighbour nodes got preempted and couldn’t cooperate with a node which is trying to leave and performance degrades and is almost similar to clh.
Microbenchmark 3 (result shown above):
10000000 array elements accessing critical section with NO non-critical section. This microbenchmark tests how mcs_tp, clh_try, clh and tas behave with increasing threads (even more than num_cores).
Important Note: In this microbenchmark and moving forward when a timeout happens for a clh_try’s queue node, it will try to check for lock holder’s preemption and perform a yield if so (rather that executing an alternate execution path like a non-critical section which it was doing in previous microbenchmarks) and then perform an immediate retry to acquire the lock.
Inference: At num_threads = 16 clh_try (with patience of approx 10 critical sections) performing better than clh. This is because of optimal number of timeouts and yeilds happens. At num_threads = 32 clh performing better than clh_try. This is possibly because more timeouts and yeilds happens so more overhead for clh_try. Even though the lock holder could make progress there is a possibility that the lock holder hands over the lock to a preempted thread(due to its own yield). Also leaving the queue gets more harder as number of threads increase(due to more probability of preemption). TAS still performs well. Remember that there is no fairness for tas lock and also no non-critical section for this benchmark. There is a high probability that the same thread attempts an acquire and acquires the lock and makes progress due to locality. It is very interesting to see that MCS-TP (with patience of approx 10 critical sections and MAX_NODES_TO_SCAN as 6) perform well even at higher number of threads. This is as expected as this lock is supposed to tolerate preemption in higher number of threads and at the same time provide reasonable fairness to requestors.
Microbenchmark 4:
Matrix multiplication with two small sized (20x20) global 2d arrays in the critical section which should fit in L1 cache. This microbenchmark tests how mcs_tp, clh_try, clh and tas behave with a very small critical section.
Inference: We infer that the critical section execution time (309000 ns) of this microbenchmark is so small that we believe even lock latency(overhead) of obtaining each lock could have significant impact on this graph. For example mcs_tp which should perform well in higher number of threads(compared to CLH), but it is performing equal to clh which means latency to obtain individual lock is affecting the performance when critical section execution time is too small. So we should use a lock like mcs_tp and clh only when the application has a significant critical section time. The individual lock overhead will be shown in the upcoming test as a proof of this theory.
Other Tests
Test 1:
We measured the overhead to acquire and release the lock immediately (empty critical section) when there is just a single thread requesting a lock and the lock is free (noone holds the lock now).
Inference:
It was interesting to see tas had the least lock latency and orders of magnitude faster than the other locks. The clh_try and clh had similar lock latency although the clh_try was having a slightly more value. We were actually surprised by the overhead of mcs_tp. Even though we knew that mcs_tp will have high lock latency but we didnt expect it to be this high. We think that is due to the more complexity of the mcs_tp’s code although we are unsure which part of the code exactly contributes to this much latency.
Test 2:
This is a simple test to observe how the MCS-TP’s runtime varies (for a fixed patience of 10 times the critical section execution time and num of threads = 64) when we change the MAX_NO_OF_NODES_SCANNED parameter. We used the microbenchmark 3 to test this.
Inference: As we expected it to be, the performance initially increases (until 8) when we increase this parameter reaches a sweet spot (at 8) and then degrades(8 to 16) and reaches saturation (16 to 60).
Test 3:
This test varies the patience interval (by varying the timeout as a factor of critical section execution time) for both mcs_tp and clh_try and finds how that affects the runtime. We used the microbenchmark3 to test this. The NUM_THREADS was set to 64. MAX_NODES_TO_SCAN was set to 8 for MCS_TP.
Inference:
The interesting result was that mcs_tp adapts well for insufficient patience like 2 times critical section compared to the clh_try (as the program was not ending in this case). This also matched the authors observation in the paper. This is because in clh_try the nodes leave the queue when timeout occurs and rejoin the queue whereas in mcs_tp the timed out nodes stay in the queue until the lock holder removes them. This difference makes it hard for clh_try to acquire the lock at small patience interval.
Test 4:
In this test we observed how the lock acquire success rate varies with number of threads for the mcs_tp (patience fixed at time of 10 critical sections and MAX_NODES_TO_SCAN = 4 and 8) and clh_try (patience fixed at time of 10 critical sections)
Inference:
We can see that the success rate drops at 16 threads. This is expected as we have set the patience for both the locks at time of 10 critical sections, so there are timeouts happening at this point. Also we can see that the success rate drops faster in case of mcs_tp when the number of threads is increased because the retries can happen for both timeouts and lock holder removing the node predicting that a preemption occurred (Unlike in clh_try where it happens only for timeouts. Also, given that we are running in GHC machine, preemption probability is high when running 16 or 32 threads, so this is a possible scenario to happen). Also the success rate drops as MAX_NODES_TO_SCAN is increased for the mcs_tp. This is expected because as this parameter is increased the lock holder can aggressively remove more queue nodes which can trigger more retries in the system thereby decreasing success rate.
Test 5:
This is the last test which we performed. We measured the cache references for all the four lock implementations using the perf tool as it will be equivalent to roughly the interconnect traffic generated in the system.
Inference: It was interesting to see that tas creates 1000 times more cache references than the other three implementations as shown in the above two graphs.
Conclusion
From the analysis above we conclude that the mcs_tp and clh_try offers useful features at the cost of some overhead. So the right lock needs to be chosen based on the desired application.

References
CMU 15-418 Slides
See 15-418 Site
Preemption Adaptivity in Time-Published Queue-Based Spin Locks
Locks Lecture WU
Pseudocode
https://www.cs.rochester.edu/research/synchronization/pseudocode/timeout.html#mcs-try
https://www.cs.rochester.edu/research/synchronization/pseudocode/ss.html#clh